| |
Let us now imagine one of those particles that
moves back and forth as the high and low pressure peaks of the wave pass. The
greater the rate at which the point moves back and forth, the greater the
frequency (f)
of the wave (defined as the number of oscillation cycles a particle makes
each second, and given the units of Hertz, Hz, which has dimensions of
(1/time)). It is the inverse of the period
(in seconds) which measures the amount of time it takes for a wave to
complete one oscillation or cycle. More generally, the distance between similar points on
successive waves is called the wavelength
λ
(in metres).
The speed at which the wave goes from one place to the other is called the
wave velocity
v
(in metres per second). Frequency, wavelength and wave velocity are
mathematically related by the equation:
The velocity of a wave in a given
medium (air, water, etc) is fixed and is related to the physical
characteristics (temperature, density, etc...) of the medium. Frequency
and wavelength, therefore, are inversely proportional to each other, i.e.
higher frequencies correspond to shorter wavelengths. Moreover, this
relation holds for any kind of wave phenomenon.
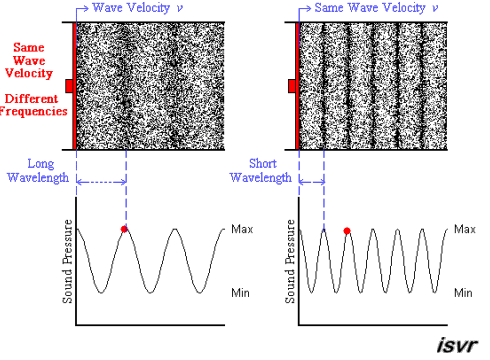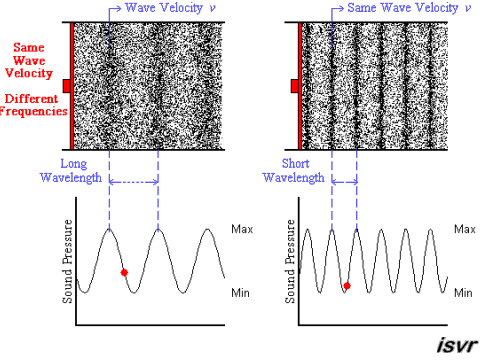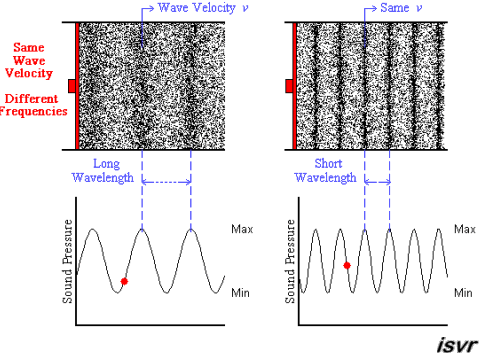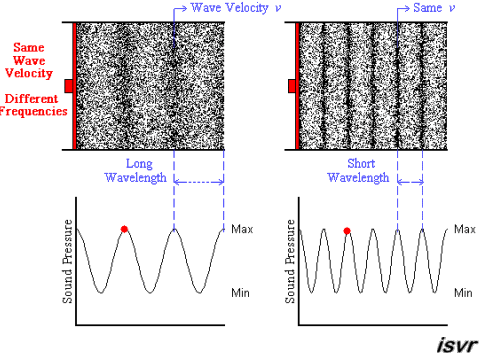
The animation below shows two acoustic
longitudinal waves with two different frequencies but travelling with the
same velocity. It can be seen that the wavelength is halved when the
frequency is doubled.
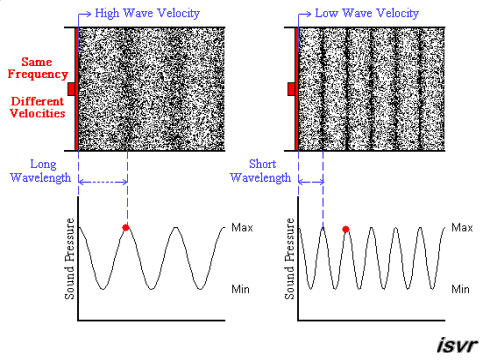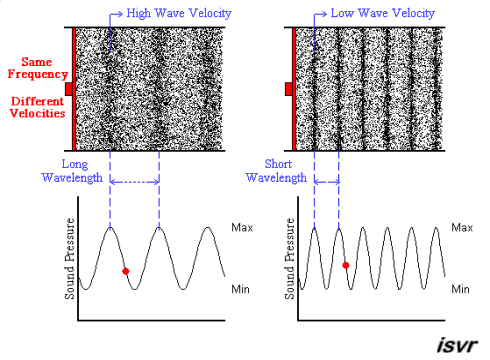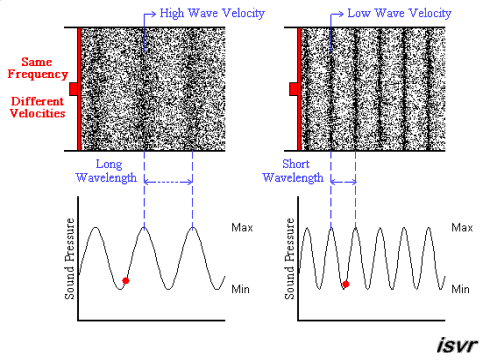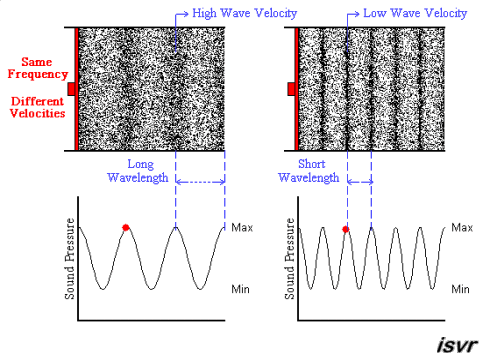
The next animation shows two acoustic
longitudinal waves with the same frequency but travelling with two
different velocities. You can see that the wavelength is halved
when the velocity is halved.
|