In this CD we will be discussing only the simplest form of waves (called linear waves). Most sound waves behave as linear waves since they produce pressure fluctuations in air that are very small compared to the atmospheric pressure. In general, waves can exhibit a much greater range of behaviour (even, for example, transforming the medium through which they propagate from one chemical to another!). For some examples of the wider range of behaviours and applications, visit the ISVR website.

A linear wave is a disturbance which travels through a medium such as air or water. Fluids such as these can be thought of as consisting of a large number of "particles", each of which consists of a vast number of molecules. Each of these particles moves to and fro as the wave travels through and it passes the disturbance on to its neighbours. However, these small parts of the medium do not travel with the wave:

Examples

Let us consider air particles set in motion by a vibrating piston. We can see that the particles (the black dots in the animation below; three of these have been coloured red for illustrative purposes) move back and forth about their equilibrium position, thus creating alternating zones of compression and rarefaction. In the rarefied region, the pressure is less than the normal undisturbed atmospheric pressure, denoted P_atm, and in the compressed region, the pressure is greater than the normal undisturbed atmospheric pressure, as shown in the animation below.  The black dots inside the piston represent small 'particles' of air, but they are not molecules.  Each particle must consist of a very large number of molecules in order to behave like a gas (or a liquid as the case may be).

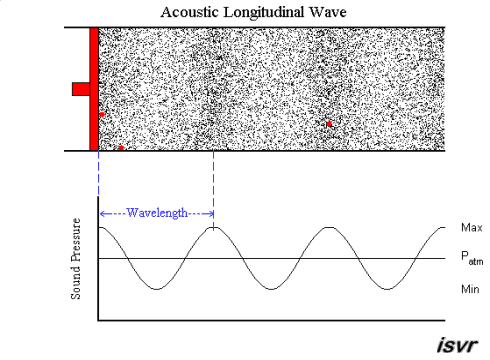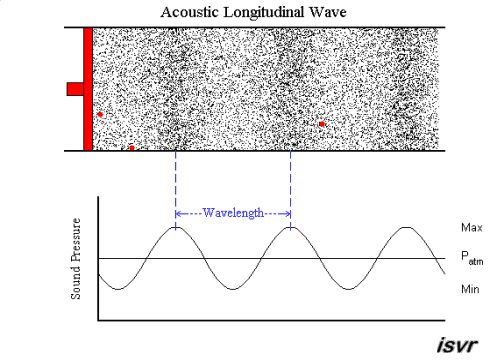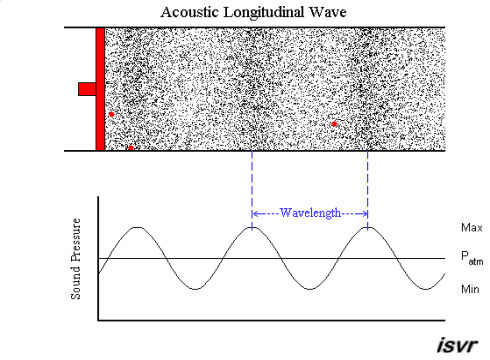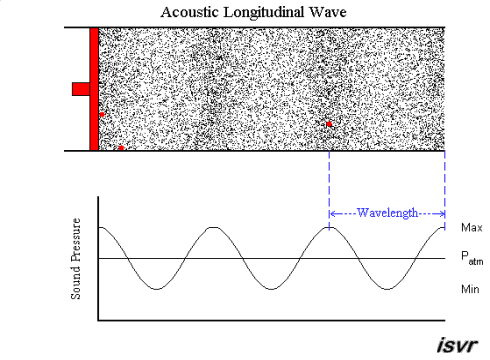
As you can see, it is the disturbance which travels, not the individual particles  (if in doubt fix your eye on one of the red particles). In sound waves, also known as acoustic waves, the local oscillations always move in the same direction as the wave. Waves like this are called longitudinal waves. Unlike acoustic waves, radio waves or guitar-string vibrations are transverse waves; that is, the local oscillations are always perpendicular to the wave motion. An example of a transverse wave is shown below, representing the waves that can be set up in, say, a skipping rope or a washing line.

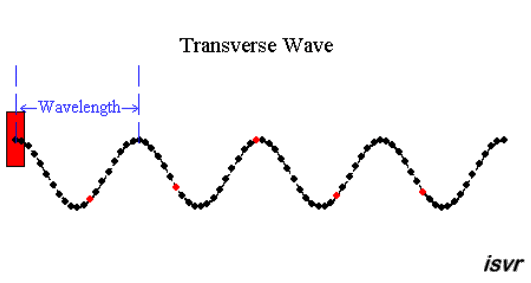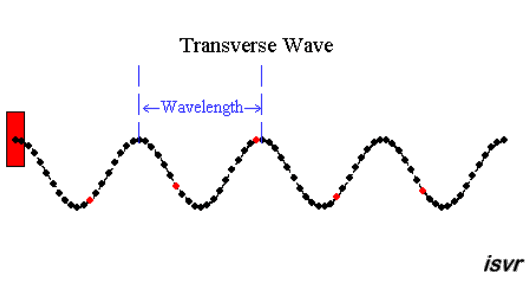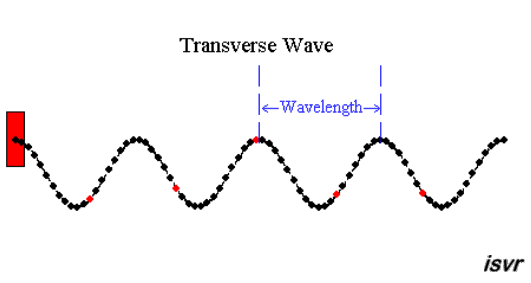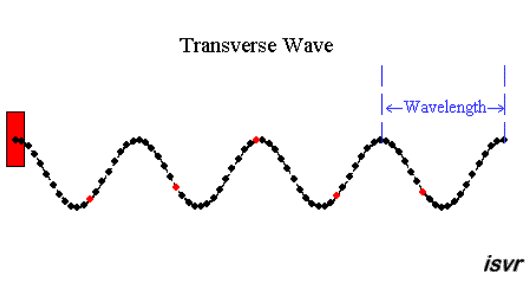
We can see from these animations that the shape of the waves repeats itself at regular distances. The distance between similar points on adjacent waves is called the wavelength λ. The speed at which the wave goes from one place to the other is called the wave velocity v.

Typically, sound waves propagate in air at room temperature at a sound speed (v) of around 340 meters per second. The range of frequencies audible to human ears lies between about 20 and 20,000 cycles per second (20 Hz to 20 kHz). The sounds that can be perceived by human ears have wavelengths in air under room conditions that range between roughly 17 mm (at 20 kHz) and 17 m (at 20 Hz).