When a guitar string is plucked, one observes that the string vibrates according to the patterns shown in the animation below. When the string is pulled to one side by the finger, the displacement of the string moves off as a travelling wave in both directions. After having reached the bridge at either end of the string, the waves are reflected back. These waves travel back and forth along the string but the resultant motion is a standing wave due to the addition of the left and right travelling components.

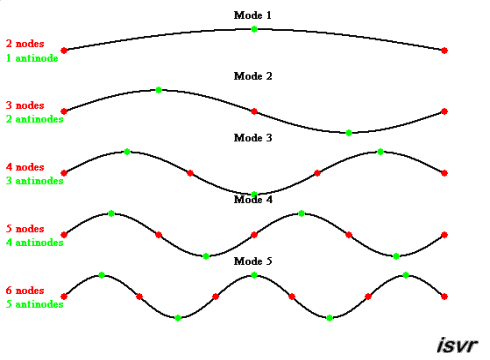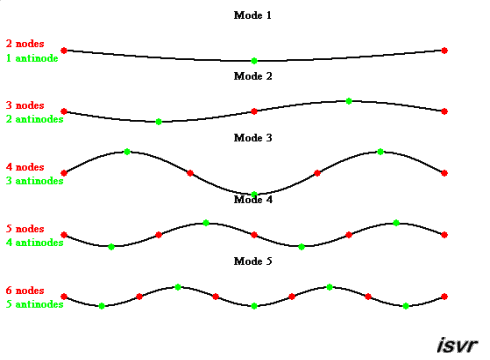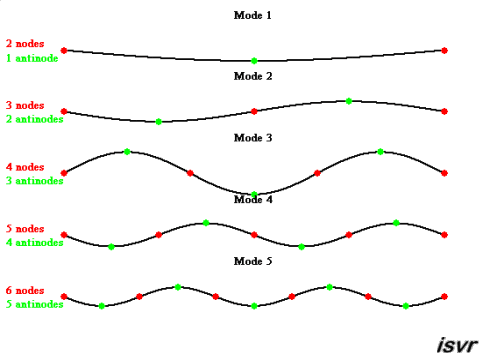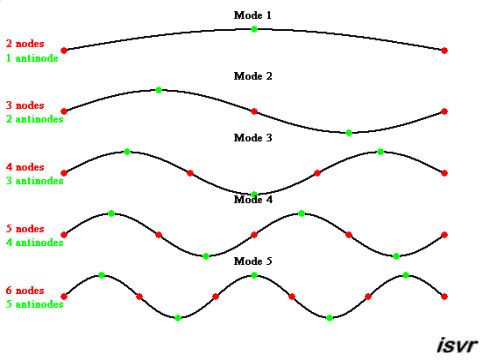
Each of these vibration patterns is called a mode. For each of these modes, there will be locations on the string with maximum displacement (displacement antinodes) and locations which do not move at all (displacement nodes). For a guitar string fixed at both ends, these modes have wavelengths related to the length of the string, L, where: λ = 2L, L, 2L/3, L/2, 2L/5,... for each of the successive modes shown in the animation below. If n is the order of the mode, the corresponding wavelength is then given by: 2L/n. Using the wavelength-frequency relationship, v = f λ , it can be seen that for each of these wavelengths, there is a corresponding frequency f = v/2L, v/L, 3v/2L, 2v/L, 5v/2L,...  Here v represents the speed of transverse mechanical waves on the string. These frequencies are also called natural frequencies of vibration of the string. When a string is excited by plucking, the resulting vibration can be thought of as a combination of several modes of vibration.