Point Sources

If the source of sound is much smaller than the wavelength of sound it emits, it can be represented by a 'point source' or 'monopole'. It will tend to radiate sound equally in all directions, that is to say, with 'spherical symmetry'. Imagine a tiny spherical source which generates sound by rhythmically expanding and contracting. When it expands a pressure wave is transmitted outwards in all directions. The pressure pulse is followed by a rarefaction pulse. The resulting sound field (due to successive compressions and rarefactions of the surrounding fluid) looks the same in all directions.

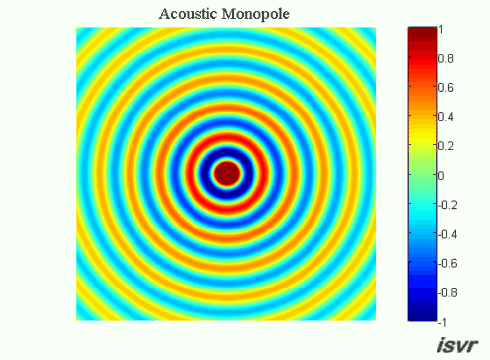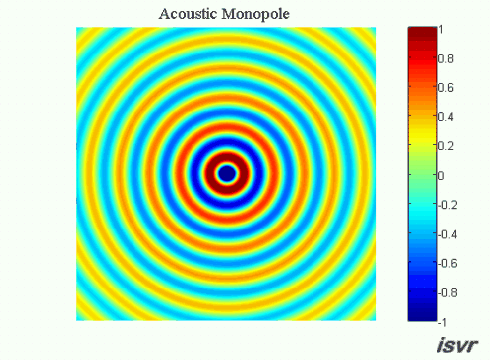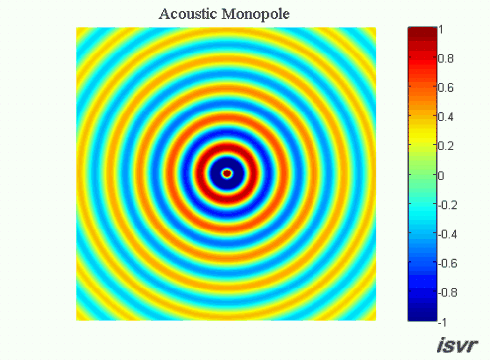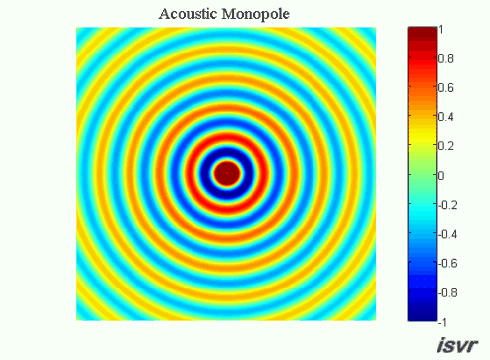
The pressure field produced by a point source is shown in the animation below. The air particles move back and forth as the spherical wave expands outwards. In practice, the point source model is a good approximation for the sound field  radiated by a loudspeaker in a sealed box at low frequencies.

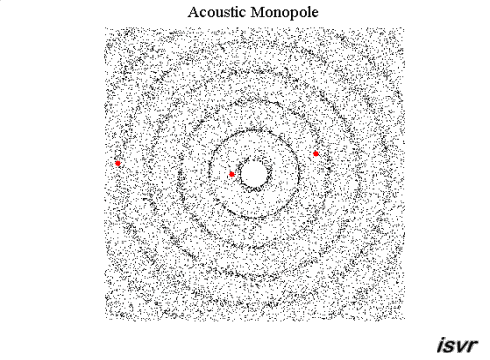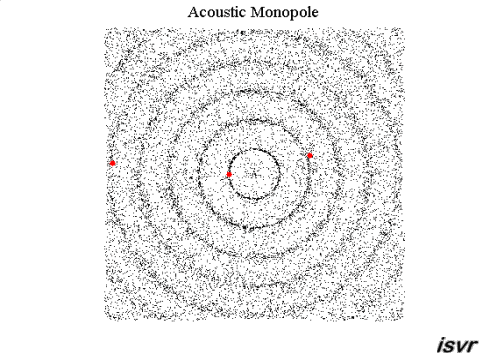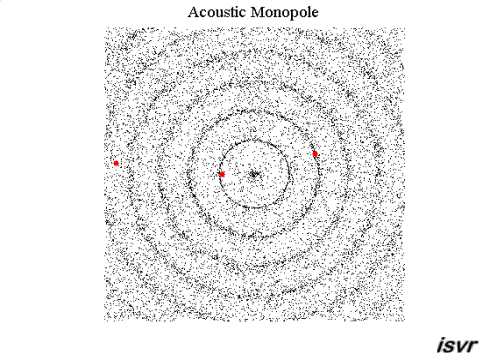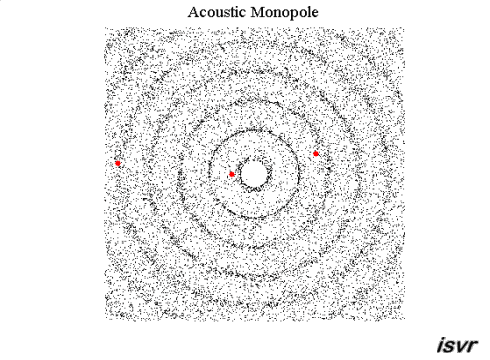
The following colour plot shows the pressure field produced by a point source. As usual with colour maps, red coloured regions represent high pressure areas and blue coloured regions correspond to low pressure areas. If you move your mouse over the animation, you can also visualize the particle displacements associated with the wave motion.

Inverse Square Law

As one moves further from a source of spherical waves, the amplitude of the sound at your location gets less. This is because of the ways in which, in travelling over the distance between the source and you, the intensity I of the wave decreases. The intensity I is the power W in the wave divided by the area A over which it is spread:

I = W/A

Assume that none of the sound wave power is absorbed (i.e. converted to heat) as it propagates from the source to you. If you are a distance r from the source, the area of the imaginary sphere over which the spherical wave is spread is  A = 4π r². Substituting this into the previous equation gives

I = W/4 π r²

where W is the power of the acoustic source. As you move further from the source, r increases and the intensity of the wave decreases. From the above equation, the intensity decreases as an "inverse-square law" with distance r, that is like 1/r². The sound-pressure amplitude of a travelling simple spherical wave is proportional to the square-root of its intensity. Therefore, in a spherical travelling wave, acoustic amplitude is proportional to 1/r. This physical law is explained by the figure below.