|

RESEARCH

TEACHING

TECHNOLOGY TRANSFER TO
INDUSTRY

UNIVERSITY OF
SOUTHAMPTON





|
|
Introduction
This page contains animations
which illustrate some basic concepts in sound and vibration. We also show
some technical applications of sound waves in scientific research,
industry and medicine.
.gif) |
Waves
|
| |
.gif) What is a wave ?
What is a wave ?
A wave is a disturbance or
variation which travels through a medium (air, water or whatever
carries the wave). Each little bit of the medium experiences some local
oscillations as the wave passes and forward the disturbance to its
neighbours. However, each parcel in the medium does not travel with the
wave: waves transfer energy without transferring matter.
Examples

Let consider air particles set in motion by
a piston. We can see that the particles move back and forth about their
equilibrium position, thus creating alternating zones of compression and
rarefaction. However, it is the disturbance which travels, not the
individual particles. In air, the local oscillations always move in the
same direction as the wave. These waves are classified as longitudinal
waves, an example of which is given by acoustic or sound
waves.

Unlike acoustic waves, radio waves or
guitar-string vibrations are transverse waves; that is, the local
oscillations are always up and down while waves travel from left to right.
We can see from the above animations that
the shape of the waves repeats itself at regular distances. The distance
between similar points on adjacent waves is called the wavelength
λ. The speed at which the wave goes from one place to the other is called
the wave velocity v.
Let's now take a look from the below
animations at the red point that bobs up and down with the crests and
troughs as the wave passes. The rapidity with which the point moves up and
down depends on the wave velocity, but also on the crest-to-crest
distance, the wavelength. A measure of how often the oscillating motion
repeats at a single place is called the frequency of oscillation,
f. Wave velocity, frequency and wavelength are related by
v = f λ
This relation holds for any kind of wave
phenomena.
Two acoustic longitudinal waves with the same wave velocity and two
different frequencies.

Two acoustic
longitudinal waves with two different wave velocities and the same
frequency.

|
| |
.gif) Sound is a mechanical wave
Sound is a mechanical wave
Sound is due to small
pressure variations of the atmosphere. Sound waves are longitudinal waves.
They propagate in air at room temperature at about 340 meters per second,
that is v = 340 m/s. The range of frequencies audible to human ears lies
between about 20 and 20,000 cycles per second (20 Hz to 20 kHz). Using the
wavelength-frequency relationship, we find that the
sounds perceived by human ears have wavelength between roughly 17 mm (at
20 kHz) and 17 m (at 20 Hz).
|
| |
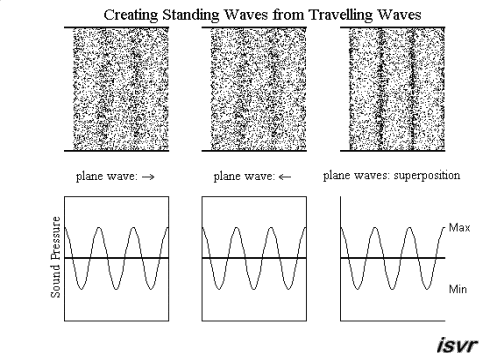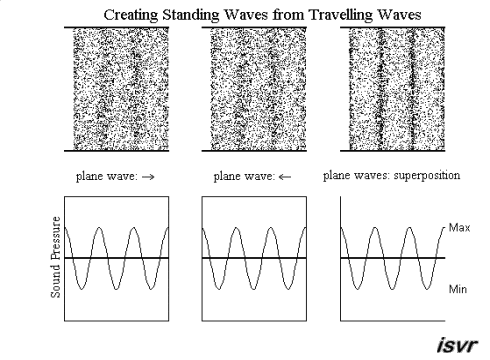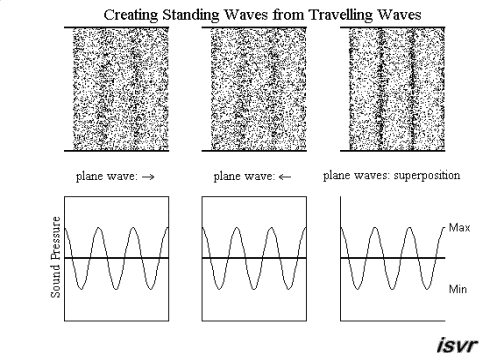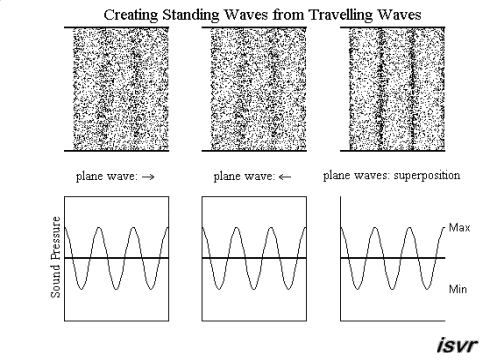
.gif) Standing wave patterns Standing wave patterns
So far, we have discussed
about travelling waves moving from one place to the other. There is,
however, a special kind of waves that stand still and only oscillate in
amplitude with time, the standing waves. They may be created from
two waves (with equal frequency, amplitude and wavelength) travelling in
opposite directions. Using superposition, the resultant wave is the sum of
the two waves. The movie below shows that the net result alternates
between zero and some maximum amplitude. Unlike the travelling waves, the
standing waves do not carry energy.
|
.gif) |
Further wave phenomena
|
| |
.gif) Dispersive waves
Dispersive waves
Waves can also propagate in
bars and plates. In this case, a remarkable fact is all waves do not
travel at the same velocity. Higher-frequency waves travel faster than
lower-frequency waves. These differences in speed causes spreading or
dispersion of wave packets, as shown in the movie below.

|
| |
.gif) Refraction of sound waves (under construction...)
Refraction of sound waves (under construction...)
|
| |
.gif) Diffraction of sound waves
Diffraction of sound waves
The animation below
illustrates how a travelling wave emitted from the upper left corner by an
airplane at take off is diffracted by a sound barrier erected to shield
homes from the traffic noise. This solution is efficient only if the
houses are located within the shadow region of the sound barrier.

 
|
.gif) |
Radiation from acoustic sources
|
|
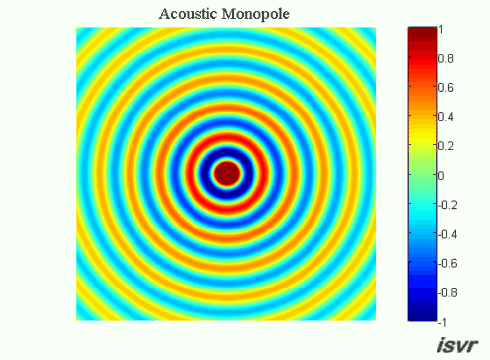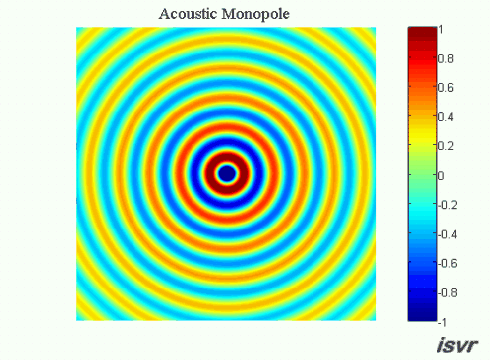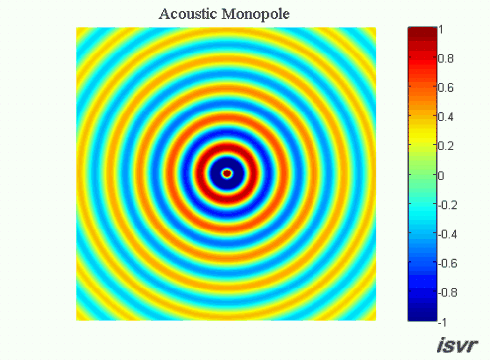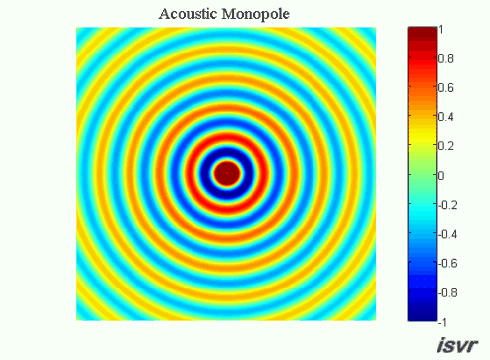
.gif) Monopole sources
Monopole sources
As an example of a monopole source, one might think of a
balloon that is rhythmically expanding and contracting. The resulting
sound field (due to successive compressions and rarefactions of the
surrounding fluid) has the same amplitude in all directions. The pressure
field produced by a monopole source is shown in the animation below. The
air particles move back and forth as the spherical wave expands outwards.
In practice, the monopole source model is a good approximation for the
sound field radiated by a boxed loudspeaker at low frequencies.

|
| |
.gif) Dipole sources Dipole sources
The simplest dipole source consists of two monopole
sources of equal strength placed a short distance apart, operating at the
same frequency but always 180o out of phase of each other [*]. An
example is given by a bare speaker cone where the volume of air pushed out
by the front side is compensated by the new volume of air that is pulled
on the back side. The animations below show that a dipole source does not
radiate sound equally well in all directions. Sound is cancelled in the
regions along the vertical axes.


How is the sound field
radiated by a dipole consisting of two monopoles when one of them is delayed with respect to the other
by the time it takes for a wave to travel from one monopole to the other ?
Answer
|
| |
.gif) The tuning fork
The tuning fork
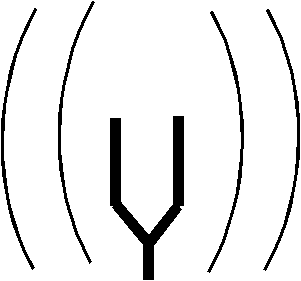
An observer holding and
rotating a sounding tuning fork at arm's length from the ear will hear two
loud regions in the plane of the tines separated by two quiet regions in
the plane perpendicular to the fork. From the animations below, it can be
seen that a similar sound field can be produced by a linear quadrupole
source. It is made of two opposite phase dipoles lying on the same
line [*].


When the observer holds and
rotates the sounding tuning fork close to its ear, he then finds four
positions where the sound is loud, alternating with four positions where
the sound is quiet. The movies below show that a lateral quadrupole
source can provide a similar sound field. It is made of four monopoles
with alternating phase located at the corners of a square [*].


|
| |
.gif) The baffled piston
The baffled piston
An important example is a
baffled piston-type source, namely a flat solid disk set in an infinite
plane baffle and moving up and down along its axis of symmetry. Analytic
expressions can be obtained to describe the sound pressure radiated in the
far-field at all frequencies. This model is used for practical baffles
such as air boxed loudspeakers.
From the animations below,
it can be seen that the radiation patterns of a loudspeaker is different
at low, medium and high frequencies.
- At low frequencies, the sound field radiated by a loudspeaker
spreads out evenly in all directions.
- At higher frequencies, the sound pressure produced by a loudspeaker is
much contained within a cone of 55o from the center axes. So,
at these frequencies, a listener will perceive higher pressure levels if
he is located in front of the speaker. If he moves to either side, he will
perceive weaker pressure levels.
- At much higher frequencies, the sound field radiated by a loudspeaker is
constricted within a cone of about 20o on either side of the
central axis. Now, the sound pressure levels fall off very rapidly as a
listener steps away from in front of the loudspeaker. In practice,
different frequencies are sent by different subwoofers and so, it is
unlikely to observe such a difference in sound levels.

|
Environmental acoustics
.gif) Room acoustics
Room acoustics
.gif) Active noise control applications
Active noise control applications
|






















