Whether the objective is to design a cross-talk canceller or a virtual source imaging system, the fundamental problem to be tackled is one of multi-channel inversion. 

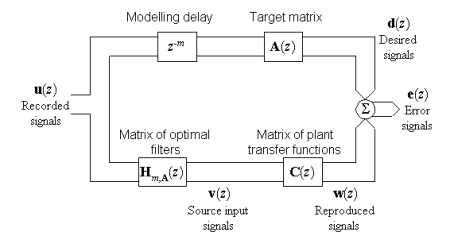
Since the inversion techniques that are usually applied to common engineering problems are not entirely appropriate for audio purposes, we have developed our own filter design methods. These methods can determine a matrix of digital finite impulse response (FIR) filters that are optimal in a quantifiable sense. The idea central to our filter design algorithms is to minimise, in the least squares sense, a cost function of the type 

The cost function is a sum of two terms: a performance error E, which measures how well the desired signals are reproduced at the target points, and an effort penalty bV which is a quantity proportional to the total power that is input to all the loudspeakers. The positive real number b is a regularisation parameter that determines how much weight to assign to the effort term. By varying b from zero to infinity, the solution changes gradually from minimizing the performance error only to minimizing the effort cost only. In practice, this regularisation works by limiting the power output from the loudspeakers at frequencies at which the inversion problem is ill-conditioned. This is achieved without affecting the performance of the system at frequencies at which the inversion problem is well-conditioned. In this way, it is possible to prevent sharp peaks in the spectrum of the reproduced sound. If necessary, a frequency dependent regularisation parameter can be used to attenuate peaks selectively. We always include a modelling delay in order to allow the optimal filters to compensate for non-minimum phase components in the plant. We do not favour the use of minimum phase approximations since these can alter the time structure of the original waveform.